Trigonometry
Trigonometry is a mathematical concept which deals with shapes and its respective angles
« Previous Next »The diagram below shows triangle ABC in which AC = 18cm, CAB = and ABC =
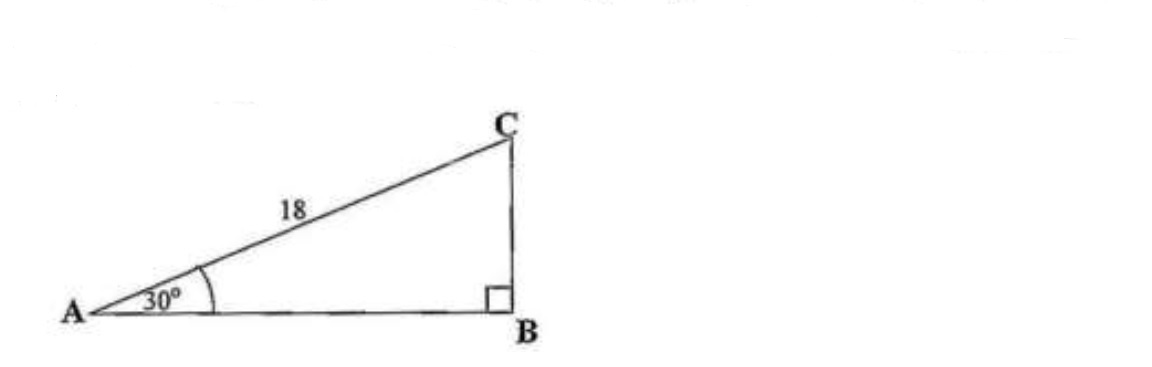
Calculate the length of BC
Solution:
AC = 18
BC = ?
Use SOH CAH TOA , which is a short name for three types of trig ratios or functions
Sin = O/H
Cos = A/H
Tan = O/A
Sin30 = O/H
O = BC
H = 18
Sin30 = BC/18
BC =
BC =
How to solve Trigonometry Example
In the diagram ABC and ACD are right angled. < ABC=< CAD= 90°. AC = 20.2cm BC = 9.5cm and AD = 12cm,
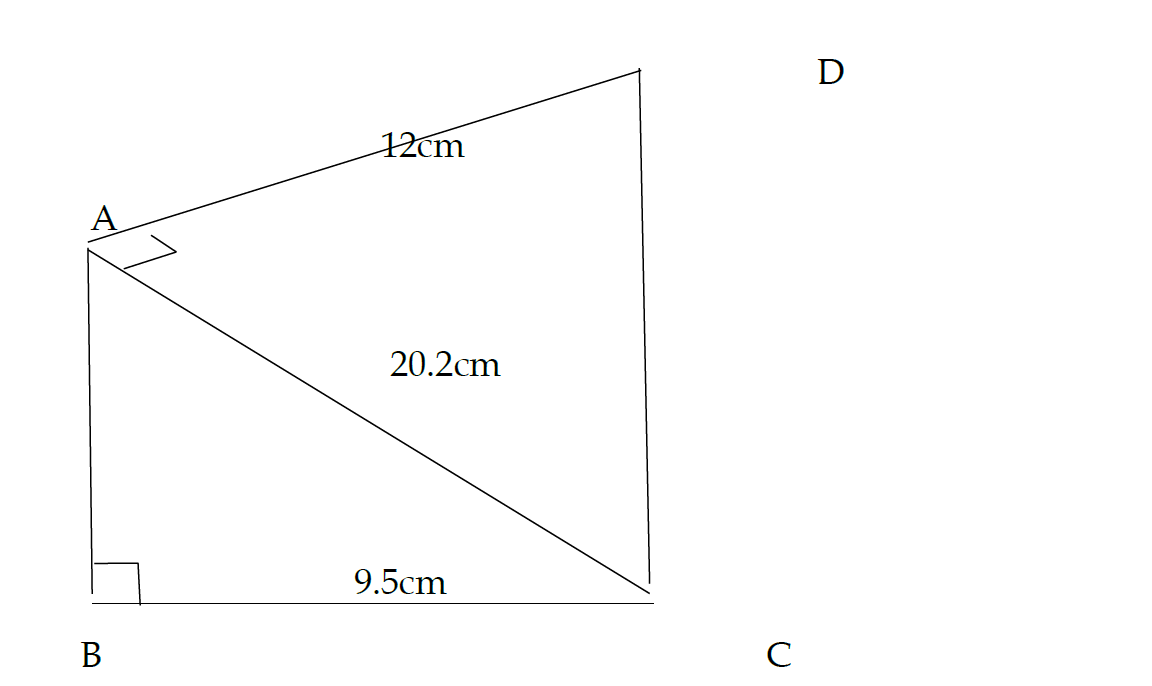
Calculate
(a) AB
(b) < BAC
(c) The area of quadrilateral ABCD
(d) The perimeter of quadrilateral ABCD.
Solutions:
(a)
AB = ? , AC = 20 , BC = 9.5
Answer:
(b)
Using SOHCAHTOA we will find angle BAC
hypotenuse = 20.2 , Opposite = 9.5 , adjacent = 17.83
We will use TOA
Tanx =
Tanx =
(c)
To find the area of the diagram above we have to know the shape of the diagram hence using the formula with respect to the diagram
Trapezium
Formula for Trapezium
a = AB, b = CD, h = 9.5
We need to find the length CD before we can find the area
hypotenuse = CD, Opposite = 20.2 , adjacent = 12
AB = 17.83, CD = 23.49, BC = 9.5
Answer:
(d)
Perimeter is the total distance around the shape
Answer:
Sine and Cosine Law
When finding the angle and distance of a triangle more than or less than the right angle triangle sine and cosine law are used. Therefore below are ways in which sine and cosine law can be applied
Sine Law

The diagram above shows how to apply sine law by deriving the following:
Sine Formula
To apply the sine law formula to solve a problem, it requires a complete pair of the length of its opposite angle to be given and also the half pair which can be the length or an angle
Cosine Law
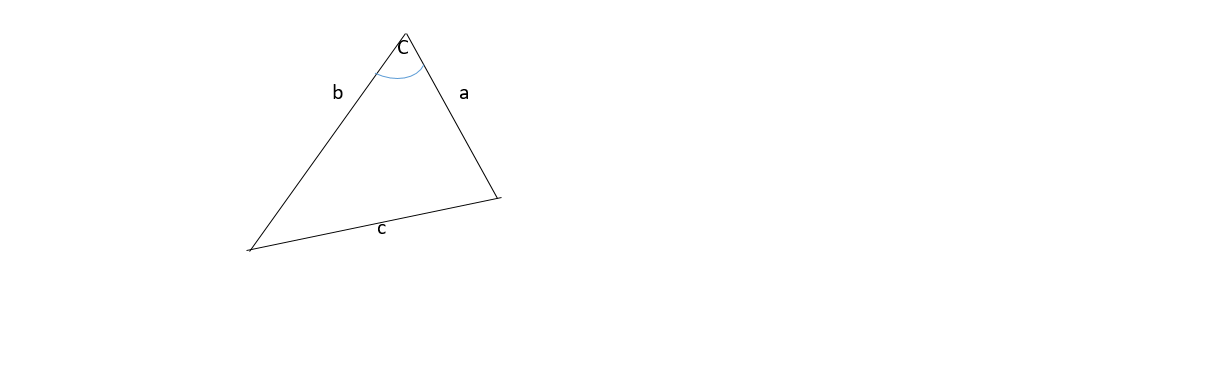
The diagram above shows a triangle having angles not equal to a right
Cosine Formula
To apply cosine law, it requires the length of two or all the sides of a triangle to be given with an angle
Area of a triangle using Sine
below is the formula of the area of a triangle, from it derive the formula of the area of triangle using sine
Sine is used to Calculate the area of any angle not just right triangle
Sine formuale of an area
Solving trigonometry using sine law
The diagram below shows the position of a Guava (G) tree, Orange (O) tree and Lemon (L) tree on a farm.
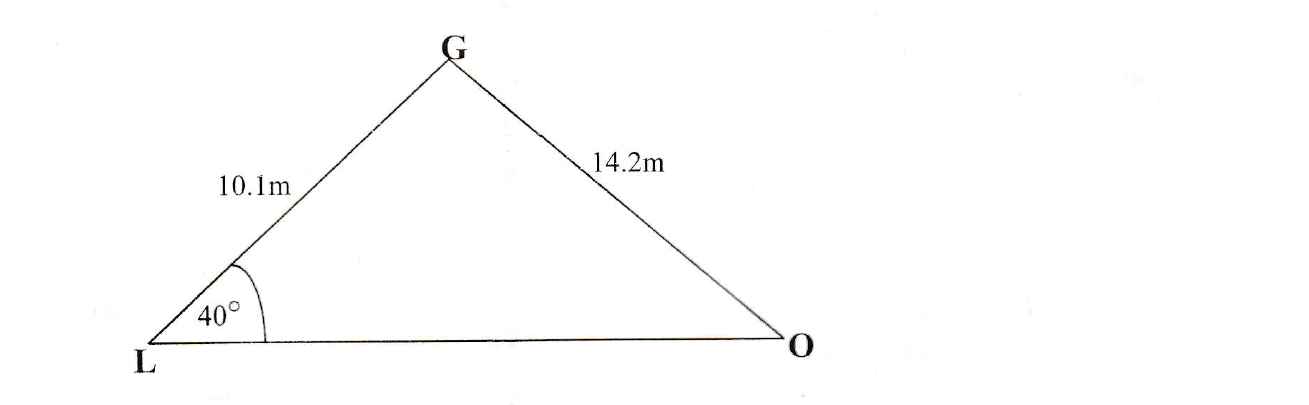
Given that LG = 10.1m, OG = 14.2m and angle OLG = 40, calculate
(i) angle OGL,
(ii) the area of triangle OGL,
(iii) the shortest distance from L to OG
Solution:
(i)
Find angle LOG first using Sine law
LOG =
OGL = 180 - GLO + LOG
OGL = 180 - 40 + 27.19
OGL = 180 - 67.19
OGL =
(ii)
To find the area use Sine method
(iii)
shortest distance from L to OG is the opposite to angle OGL and adjacent to LG , Therefore using SOHCAHTOA we can find the shortest distance
We will use SOH
Solving trigonometry using Cosine law
The diagram below shows the location of the houses for a village Headman (H), his Secretary (S) and a Trustee (T). H is 1.3km from S, T is 1.9km from H and THS =
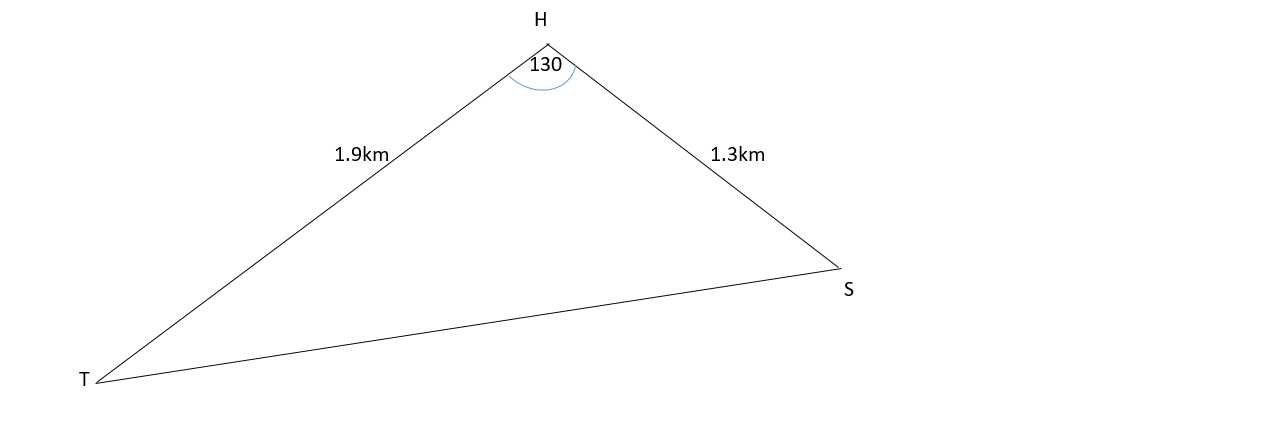
Calculate
(i) the area of triangle THS,
(ii) the distance TS,
(iii) the shortest distance from H to TS.
(iv) Find the angle between and which satisfies the equation cosx =
Solution
(i)
Area of triangle THS
(ii)
Distance TS to be found Cosine must be used
(iii)
short distance from H to TS
Find angle TSH using sine law then apply SOHCAHTOA to find the shortest distance
Given angle TSH the opposite is the shortdistance and the hypotenuse is 1.3 from SOHCAHTOA we will use SOH
(iv)
cosx =
cosx =
cos =
X =