Sets
Sets refers to the group of elements or a collection of elements
« Previous Next »Sets fundamental Concepts
From the defination of a set we can draw out two ways of representing sets namely vasual and list notation
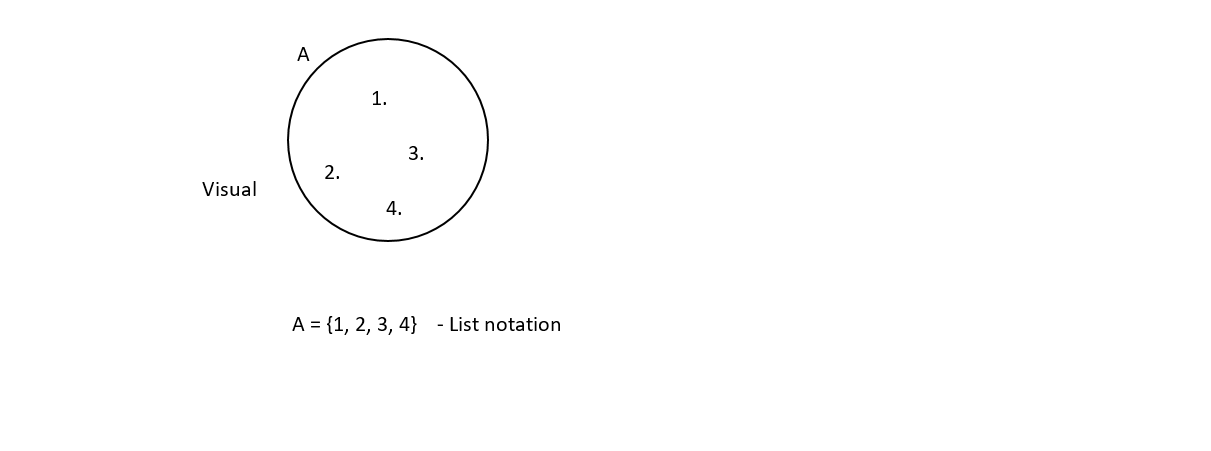
Sets can be finite or infinite
A = {1, 2, 3, 4, 5, 6, 7, 8 , 9, 10}
B = {1, 3, 4, 5, 6, 7, ...}
Set A represent a finite kind of a set stating that it has a specific start and end it indicates that set A starts with number 1 (one) and ends with number 10 (ten) from a given example
Set B is an example of an infinite set meaning that it has no end, it has started with number 1 (one) but does not have an end from the above example
Repeated elements are listed once
A = { z, n, b, a, z, z, n, a } = {a, b, n, z }
no repetitive elements should be listed more than once
There is no order in a set
{7, 2, 1} = {1, 2, 7 }
The order of a sets really does not impact the change of a given sets
Common sets
Natural numbers
below are examples of natural number
{0, 1, 2, 3, 4, ...} or {1, 2, 3, 4, ...}
Integers
below are examples of Integers these are numbers that are positive or negatives
{..., -3, -2, -1, 0, 1, 2, 3, ...}
Rational numbers
below are examples of Rational number these are fractional numbers
D = {white, black, grey }
White is an element of D , white D
Blue is not an element of D, Blue D
Cardinality of a set
The Cardinality of D is 3 (Size), |D| = 3
Cardinality refers to the number of elements which makes up a set
Empty set , = { }
Intersection sets, Union of a set and Venn diagram
Find the Intersection of the given sets
A = {3, 7, 9, 10, 12, 17}
B = {2, 3, 9, 11, 12, 18, 20 }
To find the Intersection of set A and B we have to find out the elements which are common in both sets
A B = {3, 9, 12}
Find the Intersection of the given sets
M = {a, b, c, d, e }
N = {f, g, h }
M N = { } or
Find the Union of the given sets
p = {1, 4, 5, 7, 9 }
Q = {4, 9, 10, 13 }
Union means combining these sets to a joint set
P Q = {1, 4, 5, 7, 9, 10, 13}
How to solve a venn diagram with examples
The diagram below shows three sets A, B and C. Given that (A∪B∪C)=50 find
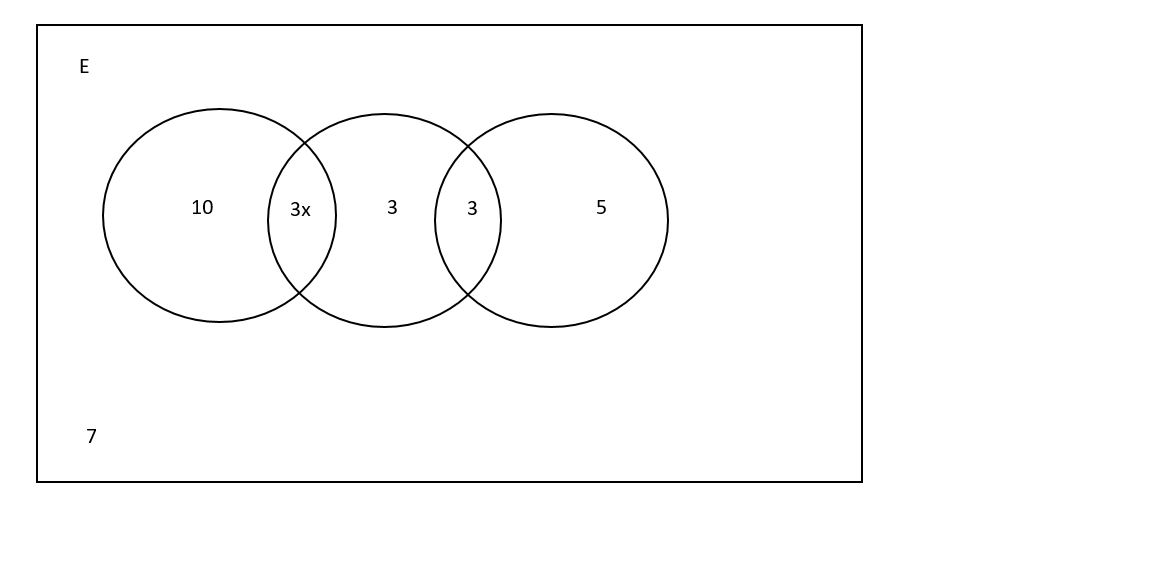
(i). the value of x
(ii).
(iii).
(iv).
Solution:
(i). (A∪B∪C)=50
(A∪B∪C)=50. This equation reads that the elements in A union B union C adds upto
Answer:
(ii). reads numbers in A union B means elements in A plus elements in set B
n(AUB) = 10 + 3x + 3 + x
Note that X = 8
n(AUB) =
n(AUB) =
Answer: n(AUB) =
(iii).
reads number of element B Union C complement, meaning elements that are not in union B and C in this case its 10 and 7
Answer:
(iv). reads A complement Intersection C complement, meaning number of elements that are not in both sets. in this case it is 3 and 7
Answer:
Venn diagram Example
Draw a venn diagram from the following sets by representing the Intersection and Union of sets
X = {6, 7, 8, 9, 10}
Y = {5, 7, 8, 11, 12}
X Y = {7, 8}
X Y = {5, 6, 7, 8, 9, 10, 11, 12}
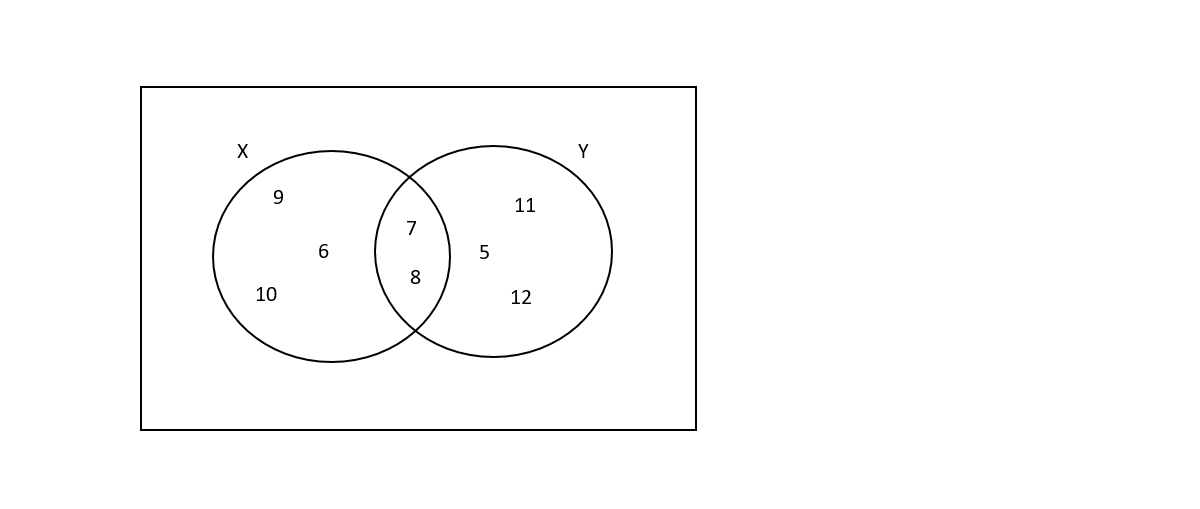
The venn diagram
The Venn diagram below shows the number of students in each of the three course at a university
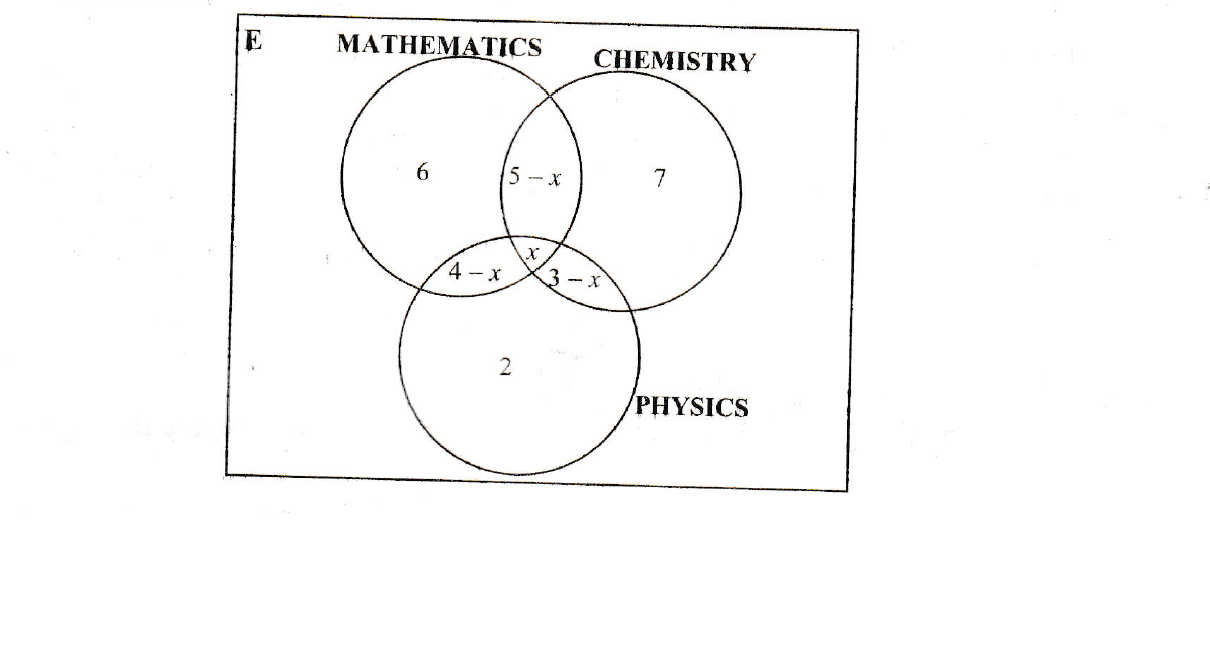
(i) Given that they where 25 students altogether, find the value of x
(ii) How many students studied
(a) Mathematics and Chemistry only
(b) One course only
(c) Chemistry and Physics but not Mathematics
Solution:
(i)
Answer:
(ii)
(a)
5 - x
5 - 1
Answer: 4 students
(b)
6 + 7 + 2
Answer: 15 students
(c)
3 - x
3 - 1
Answer: 2 students
Derive answers from a venn diagram
A survey carried out at Kamulima farming Block showed that 44 farmers planted maize, 32 planted sweet potatoes, 37 planted cassava, 14 planted both maize and sweet potatoes, 24 planted both sweet potatoes and cassava, 20 planted both maize and cassava, 9 planted all the three crops and 6 did not plant any of these crops.
(i) Illustrate this information on a venn diagram
(ii) How many farmers
(a) were at this farming block,
(b) planted maize only,
(c) planted 2 different crops ?
Solution:
(i)
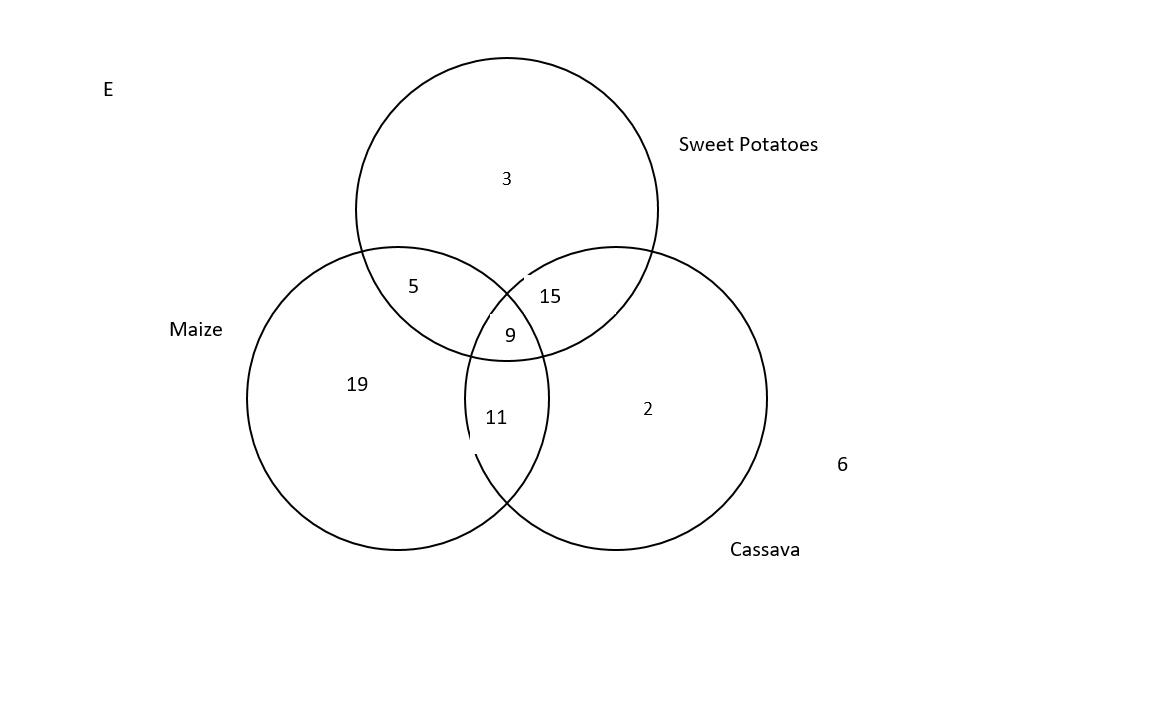
(ii)
(a)
Total number of farmers : 19 + 5 + 9 + 11 + 3 + 15 + 2 + 6 = 70
(b)
Farmers who planted maize only = 19
(c)
Farmers who planted two different types of crops 5 + 11 + 15 = 31
Download the Mathematics Sets learning materials
Are you looking to dig deeper into the fascinating world of mathematics sets? Look no further! In this mathematics for sets PDF will provide to you a comprehensive guide to sets, covering everything from the basic concepts to advanced applications. This PDF download will be a invaluable resource for you. Get ready to expand your knowledge and master the art of sets in mathematics!
ECZ Mathematics sets pdf