Pythagoras Theorem
A Pythagoras Theorem is a mathematical relation amongest three sides of a right triangle namely the hypotenuse, adjacent and opposite.
« Previous Next »The Pythagoras Theorem has the following mathematical formula
How to solve Pythagoras Theorem step by step
In the right angled-triangle ABC below find the value of x in meters(m)

Pythagoras Theorem Formula from the above diagram
BC = 7 + x , AB = 5 + x , AC = 2x
Substitute into the formula
Expand and simplify
Adding like terms on each side we have
Collecting like terms we have
Adding and subtracting
Rewriting the equation we have
From the above quadratic equation find the value of x by factorising
Simplify the quadratic equation
product = -6
Sum = -1
Factors = -3, 2
or
or
Pythagoras Example
Let AB and BC be the slant height in a diagram below. Hence find the lenth BC
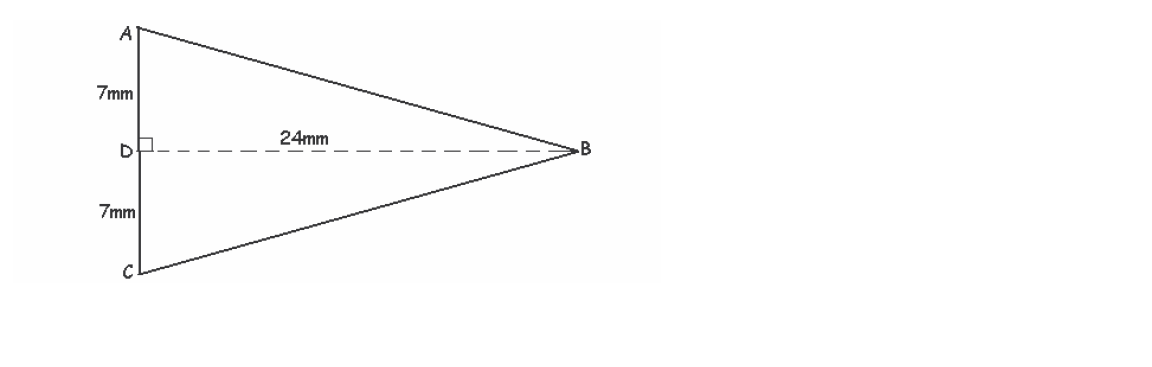
Solutions:
Given that BC = ? , BD = 24mm and DC = 7mm
Answers:
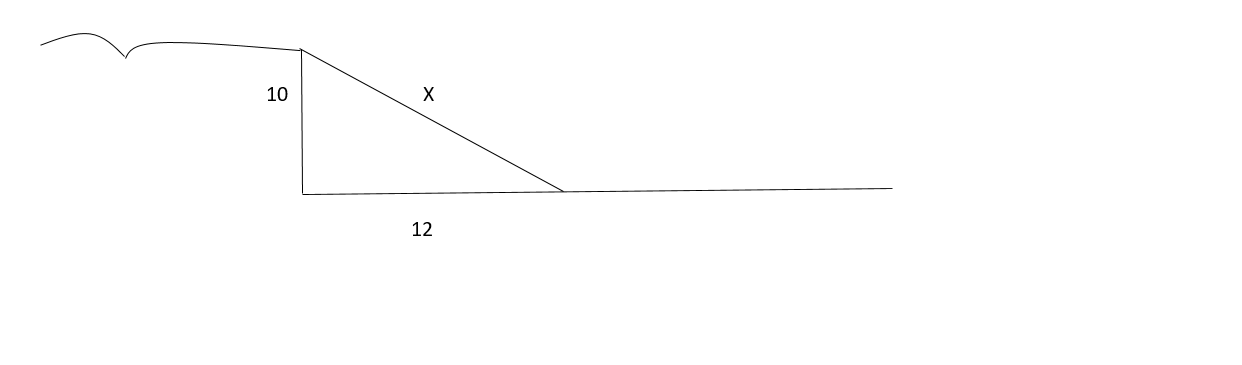
How to find distance using Pythagoras
Calculate the distance x taken by a boy to move from the cliff
How to use pythagoras theorem
Two buildings are built next to each other and are joined by a footbrigdge of lenth 20 meters and the distance between than is 15 metres. Find the height h

How to solve Pythagoras Theorem
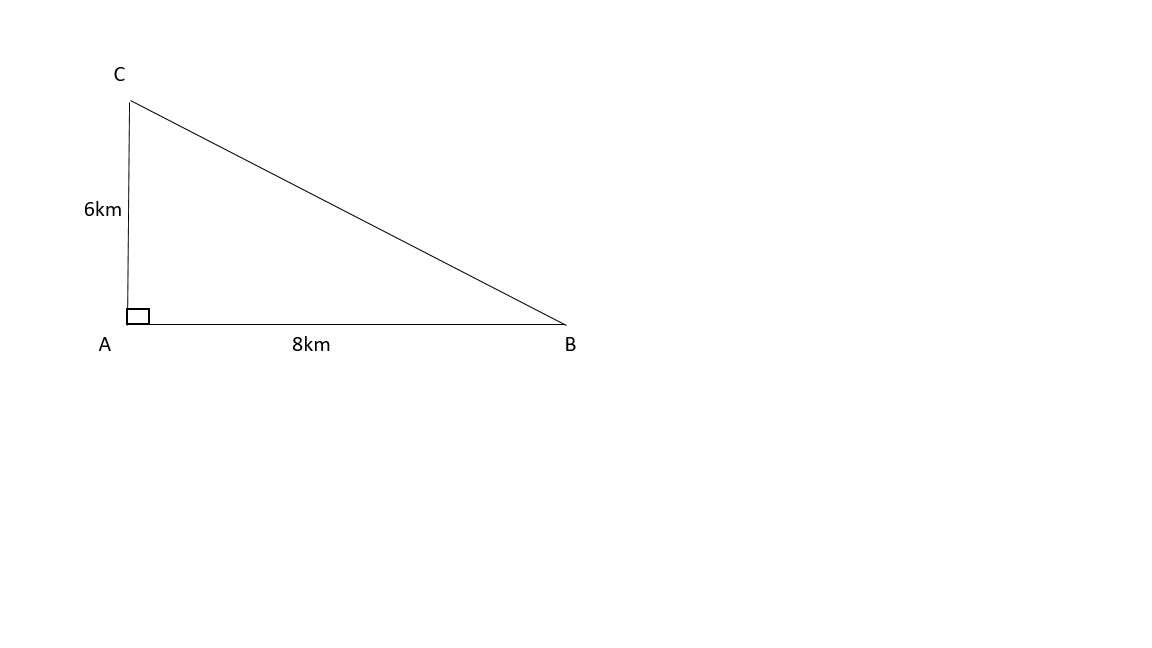
It takes 8 km for a drive to move from town B to town A and 6km from town A to town C , find the distance the drive will take to travel from time C to town B