Graph of Polynomial
A Polynomial function is an algebraic expressions that satisfied quadratic function, cubic function format ...etc
« Previous Next »How to solve Polynomial using the graph
The diagram below shows the graph of

Use the graph
(i) to calculate an estimate of the gradient of the curve at the point (2,5)
(ii) to solve the equations
(a)
(b)
(iii) to calculate an estimate of the area bounded by the curve, x = 0, y = 0 and x = -2
Solutions
(i)
Use the graph to find gradient
(2, 5) (2.5, 10)
Gradient =
X1 = 2, X2 = 2.5, Y1 = 5, Y2 = 10
Gradient =
Gradient =
Answer: Gradient =
(ii)
(a)
From the equation above .
Therefore
Draw a line on the graph. hence find the values of x at the points the line intersect the graph
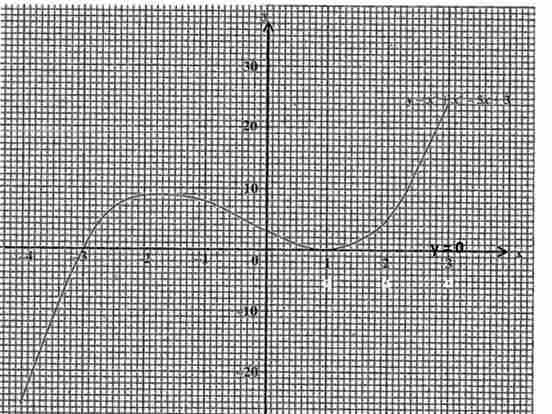
values of x at the points the line touchs the graph
Answer: (1, 0) and (-3, 0) from line
(b)
Plot the line on the graph
given that x = -3 , y = 5x (-3, -15) and x = 3, y = 5x (3, 15)
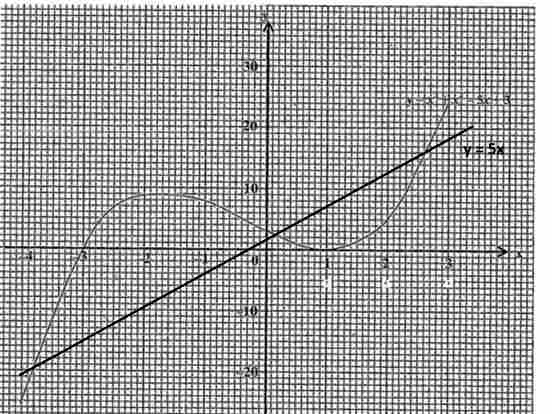
values of x at the points the line touchs the graph
Answer: (-4, -20) and (0.2, 0.2) and (2.5, 16)
(iii)
Area bounded by lines x = 0, y = 0 and x = -2
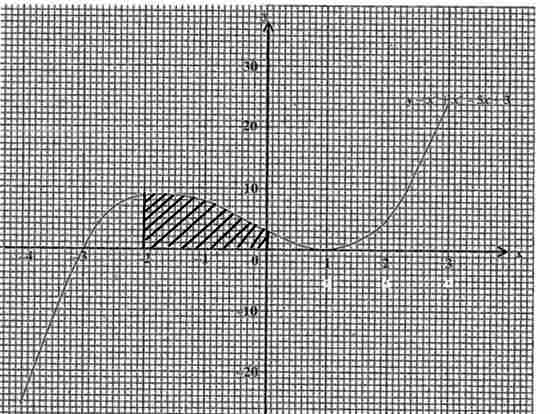
The shape of the area bounded by lines x = 0, y = 0 and x = -2 is a tripezium
Formula for area of a tripezium
Area = h
a = 2, b = 1, h = 9
Area = 9
Area = 9
Area =
Answer: Area =
How to solve Polynomial
The variables x and y are connected by the equation . some of the corresponding values of x and y are given in the table below
i) Calculate Value of r
ii) Taking 2cm to represent 1 unit on the x-axis for -3 =< x =< 3 and 2cm to represent 10 units on the y-axis for 0 =< y =< 30, draw the graph of
iii) Use your graph to calculate an estimate of the
a) gradient of the curve at the point where x = 2,
b) area bounded by the curve, x = -3 and x = -2.
Solution:
i)
Y = r
x = -1
Answer:
(ii)
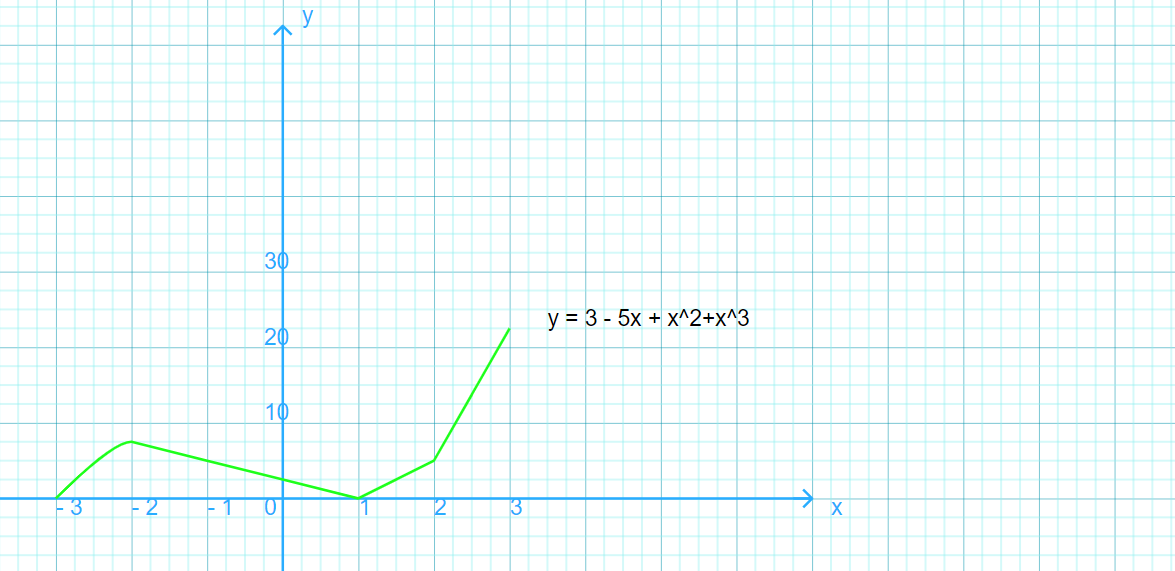
(iii) (a) and (b) using the gragh
(a)
Gradient =
(2, 5), (3, 15)
X1 = 2, X2 = 3, Y1 = 5, Y2 = 15
Gradient =
Gradient =
Answer: Gradient =
(b)
The shape of the area bounded by line x = -3 and x = -2 is a triangle, hence to find the area you have to use the formula for area of a triangle
Formula for area of a triange
Area =
b = 1 , h = 9
Area =
Area =
Answer: Area =