Geometrical Construction
Geometrical Construction is the drawing of lines, angles and shapes using Compass, ruler and Protractor
« Previous Next »Construction of Angles
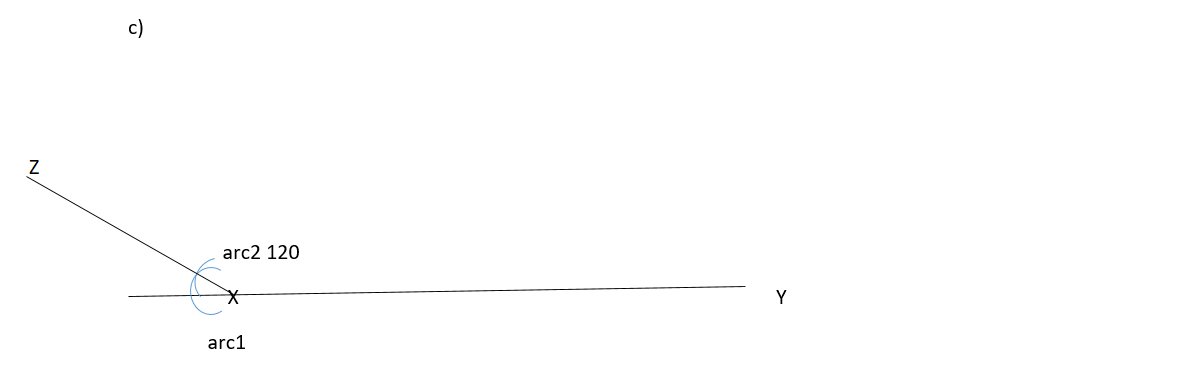
On a line segment XY = 10cm, contruct each of the following angles at X using a ruler and a pair of compasses only.
a) b) c)
Instructions to draw angle
1. From line XY put the compass at point X and create an ARC which is arc1
2. Secondly from arc1 to the point where it intersect line XY place the compass there and mark an arc2
3. Thirdly make a line XZ which is the point of interseption between the two arcs arc1 and arc2
4. Lastly angle is the angle between line XY and XZ
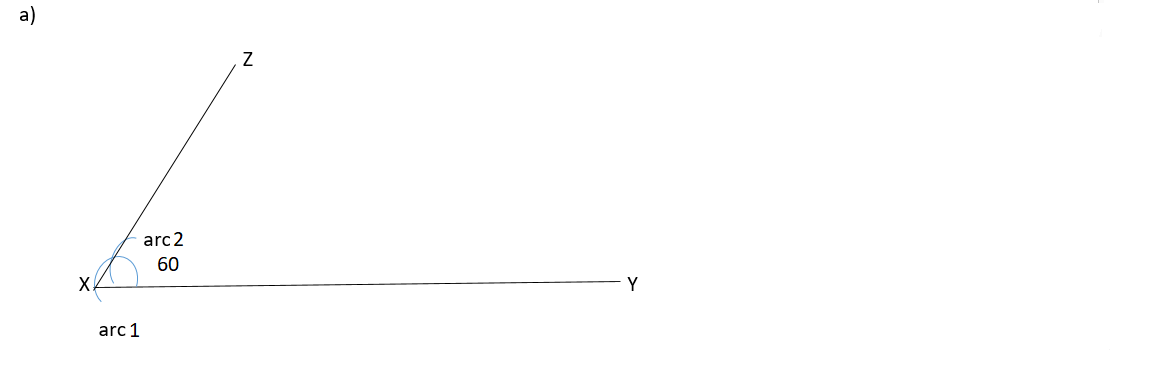
Instructions to draw angle
To make a angle you should follow the steps below
1. Starting at point X make arc1 which intersect line XY and goes beyond
2. Taking a point on the right side where arc1 intersect line XY make another arc on above which is arc2
3. From the left side of the arc1 where it intersect line XY make an arc above which is arc3
4. Therefore after creating arc2 and arc3 make a line which is the point of interseption between arc2 and arc3 line XZ. The angle created from line XY and XZ is
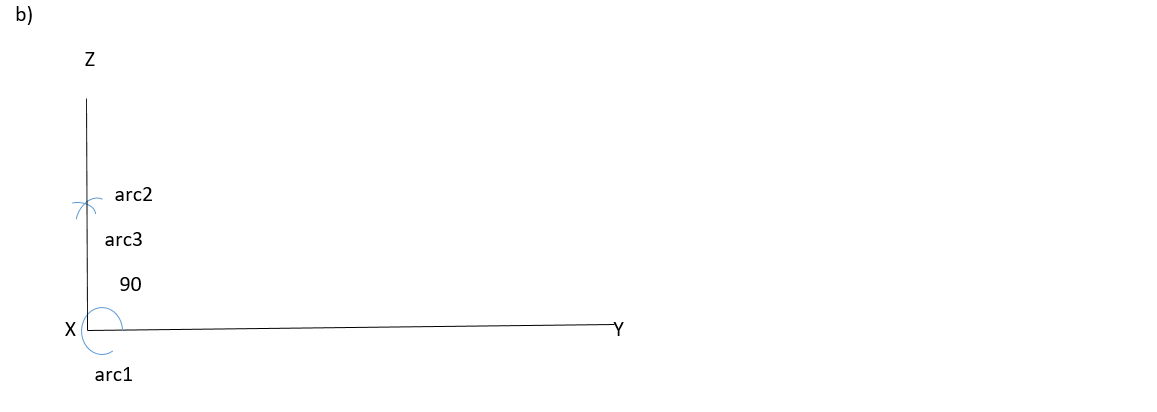
Instructions to draw angle
Making a angle you have to follow these steps
1. From point X arc1 is created where it intersect line XY
2. At the point an arc1 intersect line XY make arc2
3. The point of interseption between arc1 and arc2 is a straight line XZ. hence the line angle between the line XY and XZ is
Bisection of Angles
On a line segment MN, construct each of the following angles at M using a ruler and a pair of compass only
a) b)
Instructions to draw angle by bisection
To find angle we have to bisect angle . Bisect means cutting an angle in halves
From the we will bisect it to find . Therefore using the same compass radius (length) place the compass where arc1 intersect line XZ and draw arc3 using the same radius draw another arc by placing the compass at the point arc1 intersect line XY draw arc4
With that done draw a line of interseption between arc3 and arc4 which cuts angle in halves. hence has been found
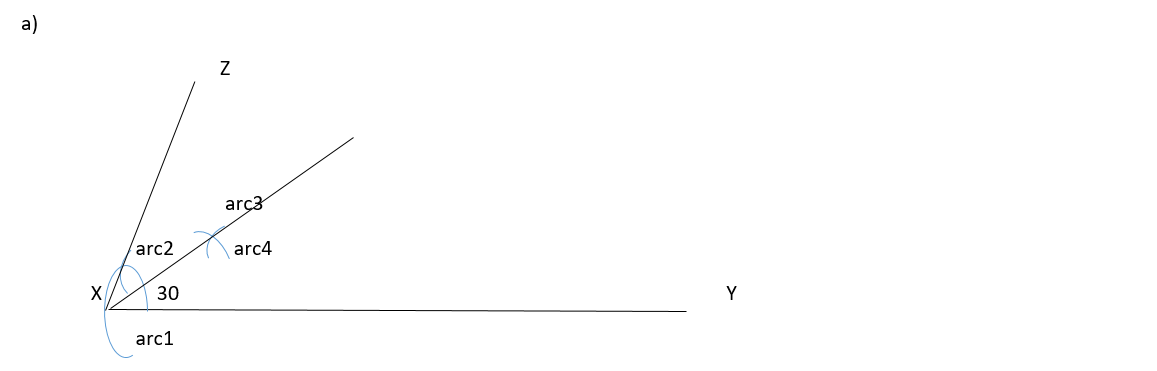
Instructions to draw angle by bisection
The second question (b) is asking us to find in order to find the angle using compass and ruler you have to know that is the half of . henceforth we have to bisect angle to find
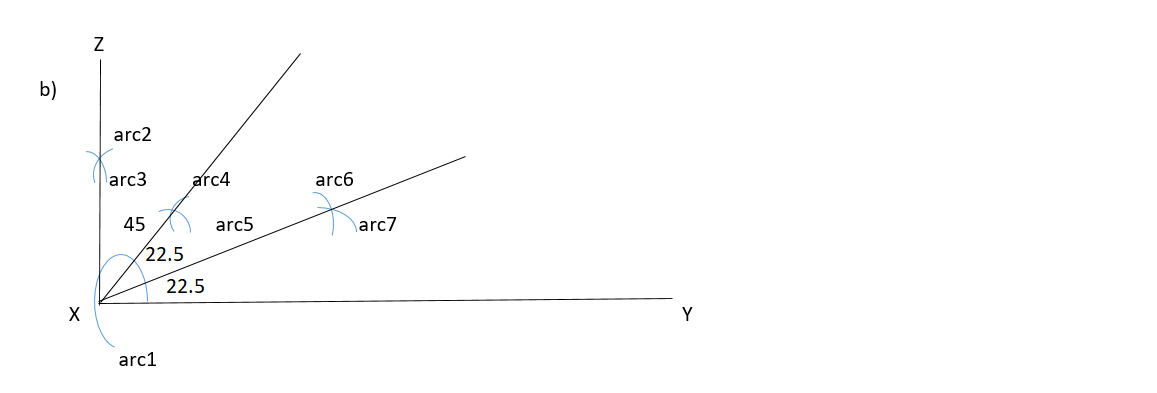
how to solve Locus of points
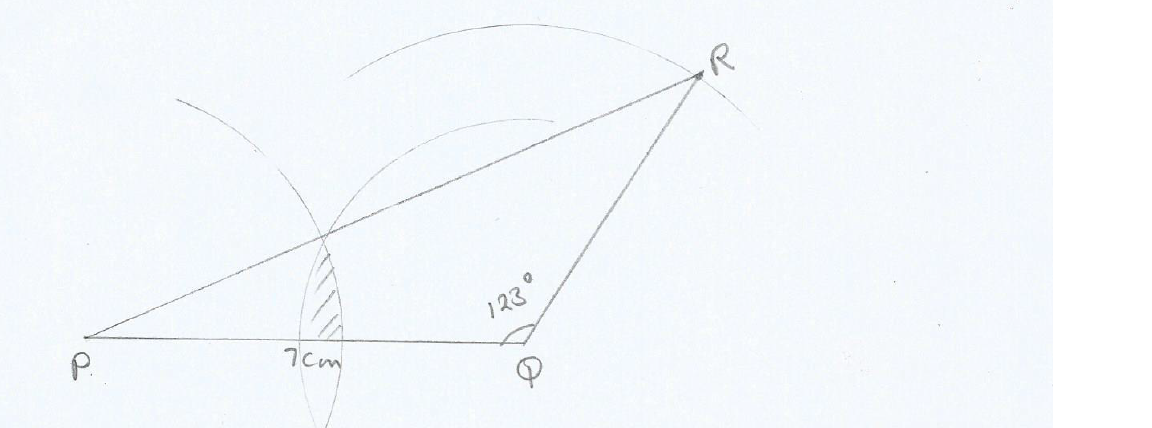
Construct a triangle PQR,in which PQ=7cm,QR=5cm and angle PQR=123°.
(i) Measure PR On the diagram construct
(ii) Locus of points 4cm from P.
(iii) Locus of points 3.5cm from Q
(iv) Show clearly on the diagram, the locus of points which lie in the triangle PQR, and lie less than 4cm from P,and lie less than 3.5cmfrom Q.
Solutions:
(i) PR = 10.5cm
answers (ii), (iii) and (iv) are in the constructed diagram below
Geometrical Construction Example
Construct triangle ABC in which AB=10cm, AC=9cm and BC=7cm, measure and write down the size of < ABC.
(a) On your diagram, draw the locus of points within the triangle which are
(i) 4cm from B
(ii) Equidistant from B and C
(b) Q is a point inside triangle ABC such that it is 4cm from B and equidistant from B and C, Label the point Q.
(c) Another point P within ABC is such that P is: Nearer to B than C Greater than or equal to 4cm from C. Indicate clearly by shading the region in which P must Lie.
Solutions:
The answers are in the constructed diagram below
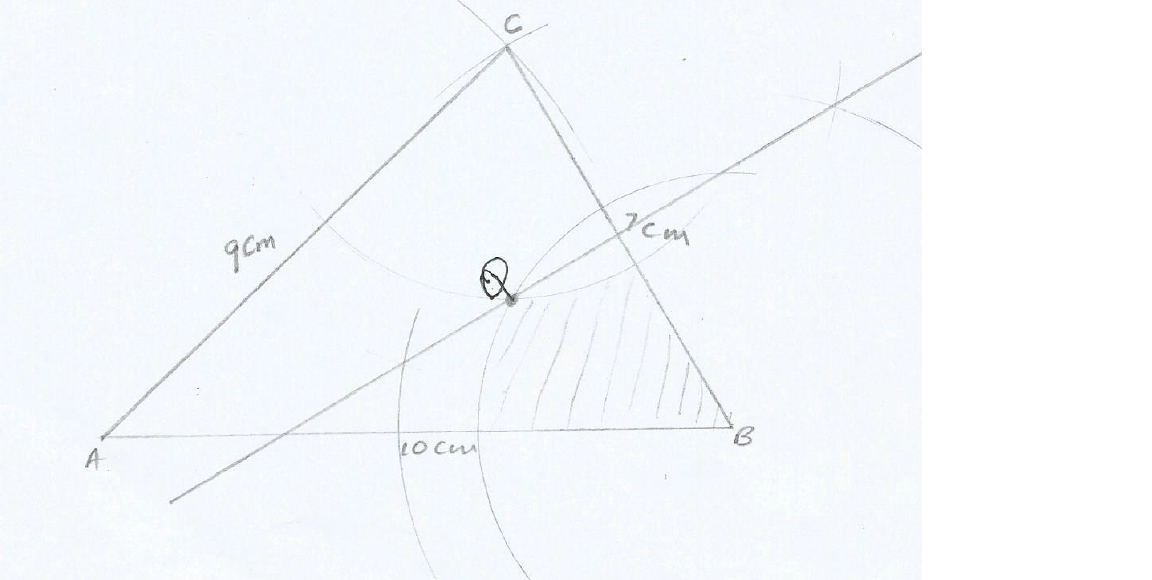
Example of Geometrical construction and finding the Equidistant
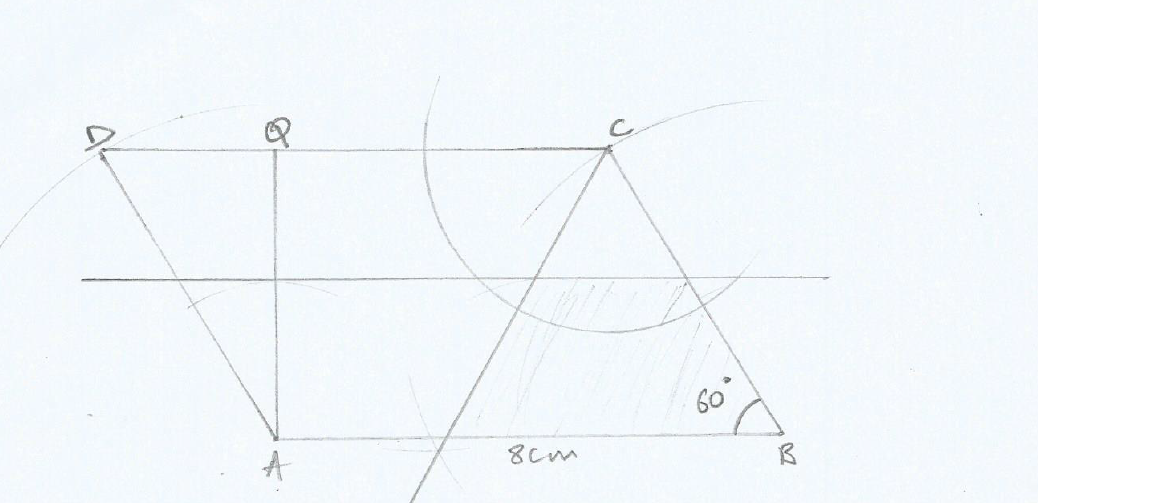
Construct Parallelogram ABCD in which AB= 8cm, BC=5.3cm and < ABC=60°.
(a) Construct a perpendicular from A to meet CD at point Q and write down the length of AQ.
(b) On your diagram, draw the locus of points within the parallelogram ABCD which are
(i) 2.5cm from AB
(ii) 3cm from C
(iii) Equidistant from BC and CD.
(c) P is the point inside parallelogram ABCD such that P is nearer to BC than CD,less than or Equal to 2.5cm from AB, indicateclearly, by shading the region in which P must lie.
Solutions
AQ = 4.5cm
Answers (b) and (c) are in the constructed diagram below
How to solve Geometric Construction
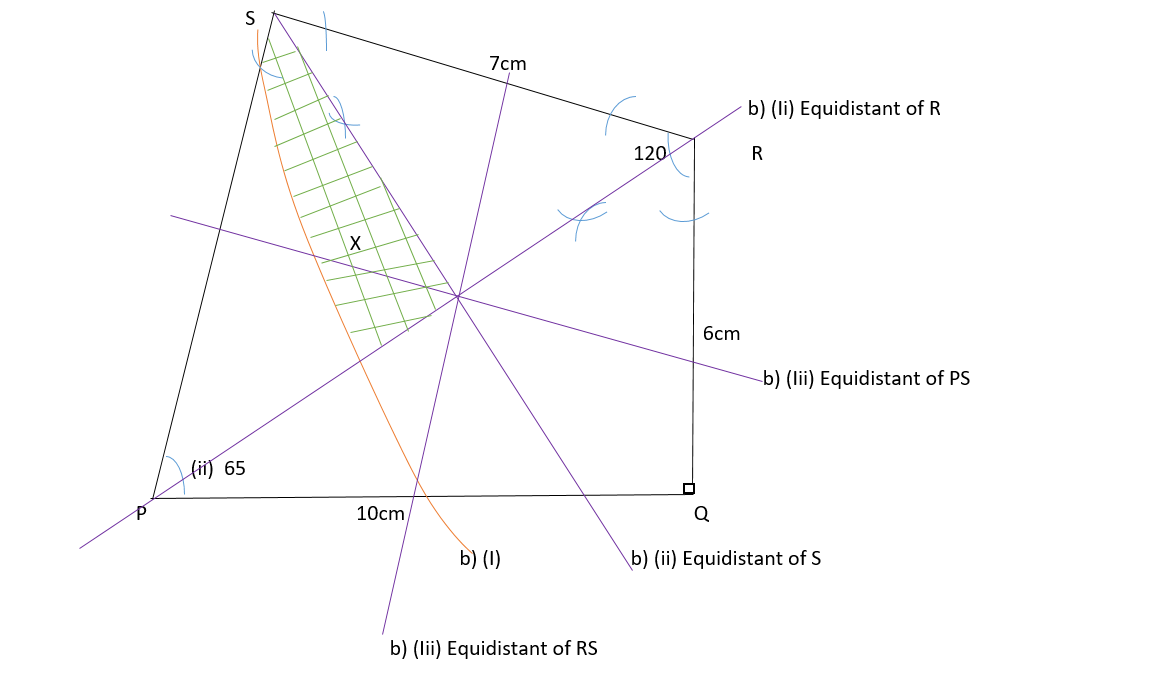
a) (i) Construct a quadrilateral PQRS in Which QR = 6cm, angle PQR = , angle QRS = , RS = 7cm and PQ = 10cm
(ii) Measure and write the size of angle QPS
b) On the diagram, draw the locus of points within quadrilateral PQRS which are
(i) 8cm from R,
(ii) Equidistant from R and S
(iii) Equidistant from PS and RS
c) A point X, within Quadrilateral PQRS, is such that it is less than or equal to 8cm from R, near to S than R and nearer to PS than RS. Shade the region in which X must lie.
Solution
Terms to note
1. Locus of point: is the set of points that represent and meets a particular condition. Example on question b) (i) the condition states 8cm from R, Therefore we have to get a compass and measure 8cm by putting the pointer on 0cm then we will place the pointer on R on the given diagram the draw the line thats intersect the diagram. by doing so you have find the locus of points
2. Equidistant: means find the equal distance from the given points on the diagram and then draw the line that indicates the equal distance. To find the equidistant of two lines joined by an angle we have to bisect the angle and then draw a line to indicate equidistant.