Speed, Velocity and Acceleration

Distance and Displacement

Distance is defined as the total length taken between two points

- It is a scalar. meaning it is a quantity having magnitude only.

Displacement is defined as the change of position of a point in a particular direction

- It is a vector. meaning it is quantity having both magnitude and direction

SI units of both distance and displacement are metre [m].

Example 1

A car moves 5km to the East and 3km to the North. What is the distance and the displacement of the car?

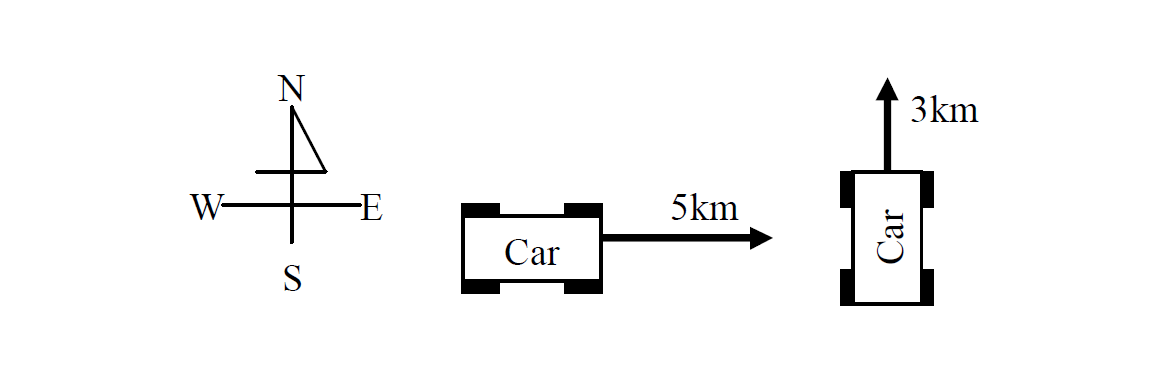
Solutions

- Distance of the car is 8km (= 5km +3km).

- Displacement of the car is 5km East and 3km North.

Example 2

The circumference of a roundabout is 10m and the car turns it once. What is the distance and the displacement of the car?

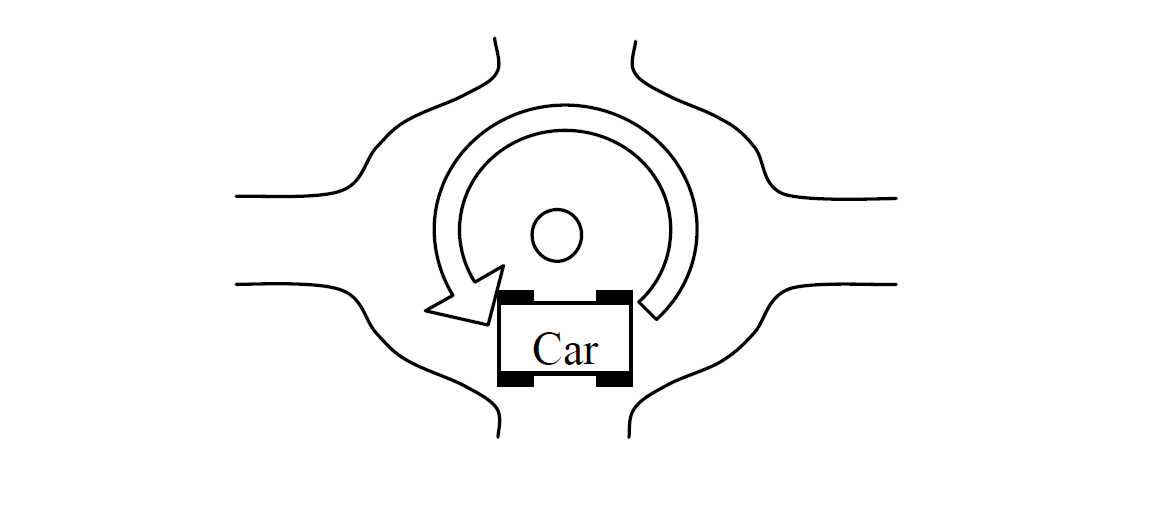
Solutions

- Distance of the car is 10m

- Displacement of the car is 0m because it came back to the starting position

Example 3

You walk forward 15m and backward 5m. What is your distance and your displacement?

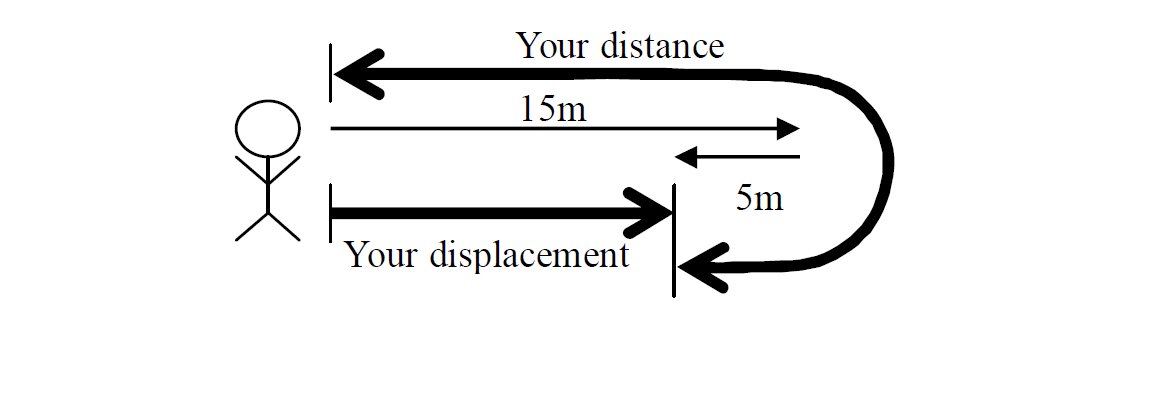
Solutions

Your distance is 20m (= 15m + 5m).

Your displacement is 10m (= 15m - 5m) forward.

Speed

Speed is defined as the rate of change of distance traveled with time. It is a scalar.

The unit of speed is metre per second [m/s].

Formula for Speed

$\mathrm{Speed}=\frac{\mathrm{Distance\; traveled}}{\mathrm{Time\; taken}}$

$\mathrm{Average\; Speed}=\frac{\mathrm{Total\; distance\; traveled}}{\mathrm{Total\; time\; taken}}$

Example

A car travels a distance of 540km from Lusaka to Katete in 10 hours. Find the average speed in km/hr and m/s.

Solution

$\mathrm{Average\; Speed}=\frac{\mathrm{Total\; distance\; traveled}}{\mathrm{Total\; time\; taken}}$

given that:

Total distance traveled = 540km

Total time taken = 10hrs

$\mathrm{Average\; Speed}=\frac{\mathrm{540}}{10}$

Answer: $\mathrm{Average\; Speed}=\mathrm{54}$ Km/hr

or $\mathrm{Average\; Speed}=\frac{\mathrm{540000m}}{\mathrm{36000s}}$

Answer $\mathrm{Average\; Speed}=\mathrm{15}$ m/s

Velocity

Velocity is defined as the rate of change of displacement with time. It is a vector.

The unit of velocity is metre per second [m/s]. (It is the same unit as speed.)

Example

What are their speeds and their velocities?

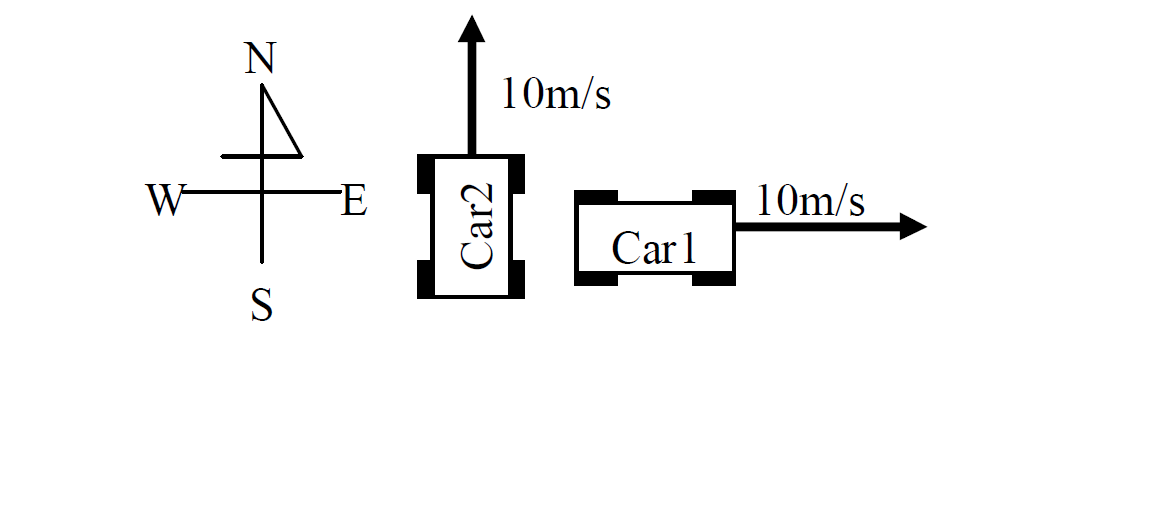
Solution

They have the same speeds of 10m/s but they have different velocities.

Car1 has the velocity of 10m/s East.

Car2 has the velocity of 10m/s North.

Acceleration

Acceleration is defined as the rate of change of velocity with time. It is a vector.

The unit of acceleration is metre per second squared [m/s2].

Formula for Acceleration

$a=\frac{\mathrm{V\; -\; U}}{\mathrm{t}}$

a: Acceleration [m/s2]

v: final velocity [m/s]

u: initial velocity [m/s]

t: time taken [s]

Example 1

A car starting from rest increases its velocity uniformly to 15m/s in 5s. What is its acceleration?

Solution

Given that

V = 15 m/s

U = 0 m/s

t = 5s

$a=\frac{\mathrm{V\; -\; U}}{\mathrm{t}}$

$a=\frac{\mathrm{15\; -\; 0}}{5}$

$a=\frac{\mathrm{15}}{5}$

Answer:

Example 2

If a car slows down from 72km/hr and stops in 10s, calculate the acceleration

Solution

Convert 72km/hr to m/s

$\mathrm{72\; km}\mathrm{1\; hr}$

$\mathrm{72000m}3600$

$\mathrm{20}1$

$\mathrm{20m/s}$

Therefore the data is:

V = 0m/s

U = 20m/s

t = 10s

$a=\frac{\mathrm{V\; -\; U}}{\mathrm{t}}$

$a=\frac{\mathrm{0\; -\; 20}}{10}$

$a=\frac{\mathrm{-\; 20}}{10}$

Answer:

When the velocity reduces, the acceleration becomes a negative number. The acceleration is called the retardation or deceleration.

Uniformly accelerated liner motion

If a body moves with a uniform acceleration (the acceleration is constant), three important equations are given below.

Formulas for uniform acceleration

1. $V=\mathrm{u\; +\; at}$

2. $x=\mathrm{ut}+\frac{1}{2}{\mathrm{at}}^2$

3. $V^2=u^2\mathrm{+\; 2ax}$

Note that:

a: Acceleration [m/s2]

v: final velocity [m/s]

u: initial velocity [m/s]

t: time taken [s]

x: distance covered [m]

Example 1

A car traveling at 10m/s accelerates at 2m/s2 for 3s. What is its final velocity?

Solution

Formula

$V=\mathrm{u\; +\; at}$

Given that

U = 10m/s

t = 3s

a = ${\mathrm{2m/s}}^2$

V = ?

$V=\mathrm{10\; +\; 2(3)}$

$V=\mathrm{10\; +\; 6}$

Answer: $V=\mathrm{16m/s}$

Example 2

A motorcycle starting from rest acquires a velocity of 72km/hr in 5s.

(a) What is its acceleration?

(b) How far does it travel during this time?

Solutions

(a)

Given that

V = 72km/hr = 20m/s

U = 0m/s

t = 5s

a = ?

$a=\frac{\mathrm{V\; -\; U}}{\mathrm{t}}$

$a=\frac{\mathrm{20\; -\; 0}}{5}$

$a=\frac{\mathrm{20}}{5}$

Answer: $a={\mathrm{4m/s}}^2$

(b)

Given that

u = 0m/s

t = 5s

a = 4m/s2

x = ?

$x=\mathrm{ut}+\frac{1}{2}{\mathrm{at}}^2$

$x=\mathrm{0(5)}+\frac{1}{2}{\mathrm{4(5)}}^2$

$x=0+\frac{1}{2}\mathrm{4\; (25)}$

$x=\frac{1}{2}\mathrm{100}$

$x=\mathrm{50m}$

Note that: You can't use the formula: D=S×T. Because there is no acceleration.

Example 3

The velocity of an object is uniformly reduced from 50m/s to 30m/s. If the deceleration is –4m/s2, how much is the distance of the body decelerating?

Solution

Given that

u = 50m/s

v = 30m/s

a = -4m/s2

x = ?

$V^2=u^2\mathrm{+\; 2ax}$

${\mathrm{30}}^2={\mathrm{50}}^2\mathrm{+\; 2(-4)x}$

$\mathrm{900}=\mathrm{2500}\mathrm{-\; 8x}$

$\mathrm{900\; -\; 2500}=\mathrm{-\; 8x}$

$\mathrm{-\; 1600}=\mathrm{-\; 8x}$

$\frac{\mathrm{-\; 8x}}{-8}=\frac{\mathrm{-\; 1600}}{-8}$

$x=\mathrm{200m}$

Acceleration due to gravity

All objects accelerate uniformly towards the earth if air resistance is ignored. It is called acceleration due to gravity. It is represented by the symbol ‘g’.

g = 9.8m/s2 ≈ 10m/s2

Points to note

1. If a stone is dropped from the top of a tall building, it accelerates uniformly downwards. If you release a stone without applying force, it starts from rest. It is called free fall.

Free fall

u = 0m/s

a = g = 10m/s2

2. If you throw up a stone, the stone decelerates to the top. Then it stops momentarily at the top. And then it starts falling freely

Throwing up

v = 0m/s

a = -g = -10m/s2

Example 1

A body falls freely from rest. Air resistance is ignored. (g = 10m/s2)

(a) What is its velocity after 1s?

(b) How far does it reach in 1s?

Solutions

(a)

Given that

u = 0m/s

a = g = 10m/s2

t = 1s

v = ?

$V=\mathrm{u\; +\; at}$

$V=\mathrm{0\; +\; 10(1)}$

Answer: $V=\mathrm{10m/s}$

(b)

Given that

u = 0m/s

a = g = 10m/s2

t = 1s

x = ?

$x=\mathrm{ut}+\frac{1}{2}{\mathrm{at}}^2$

$x=\mathrm{0(1)}+\frac{1}{2}{\mathrm{10(1)}}^2$

$x=0+\frac{1}{2}\mathrm{10(1)}$

$x=\frac{1}{2}\mathrm{10}$

Answer: $x=\mathrm{5m}$

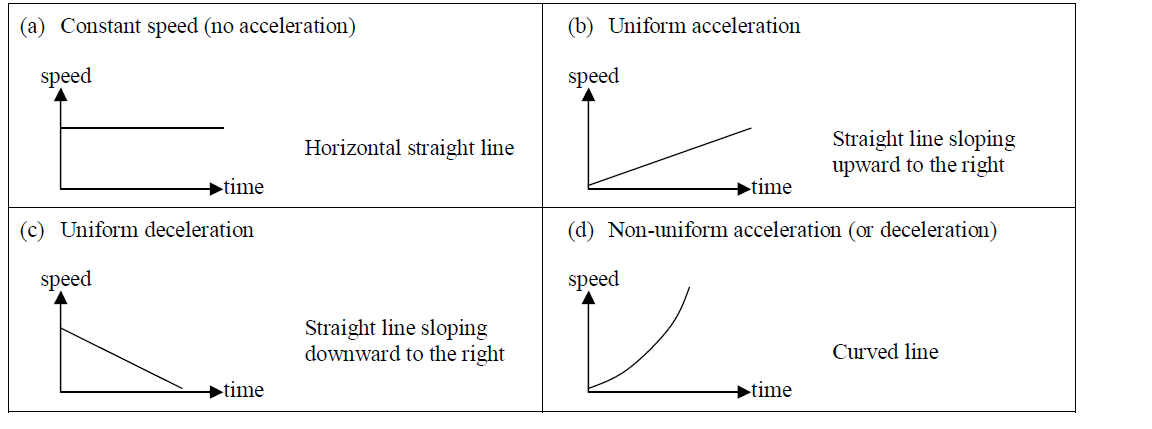
Speed (velocity) – time graph

Speed (velocity) – time graphs tell stories about the movement of an object.

- The gradient of the speed – time graph is equal to the acceleration of the object.

- The area under the speed – time graph represents the distance traveled by the object.

The diagrams below show the speed – time graphs for different kinds of motion.

Example

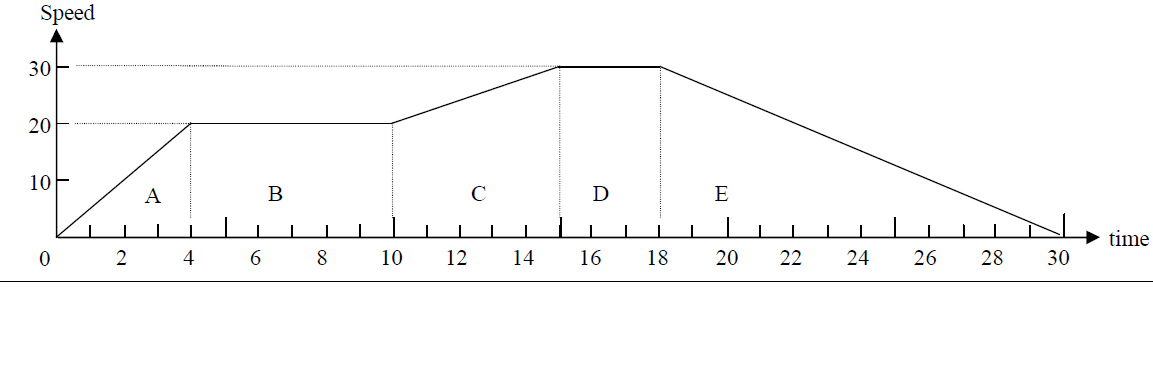
A car moving from rest acquires a velocity of 20m/s with uniform acceleration in 4s. It moves with this velocity for 6s and again accelerates uniformly to 30m/s in 5s. It travels for 3s at this velocity and then comes to rest with uniform deceleration in 12s.

(a) Draw a speed – time graph

(b) Calculate the total distance covered.

(c) Calculate the average speed.

Solutions

(a)

(b)

To find the total distance covered, calculate the area under the speed – time graph.

Area A = triangle = $\frac{1}{2}\mathrm{bh}$ $\frac{1}{2}4\times \mathrm{20}=40$

Area B = rectangle = $\mathrm{lb}$ = $6\times 20=\mathrm{120}$

Area C = trapezium = $\frac{1}{2}\mathrm{(a\; +\; b)\; h}$ = $\frac{1}{2}\mathrm{(20\; +\; 30)\; 5}=125$

Area D = rectangle = $\mathrm{lb}$ = $3\times 30=\mathrm{90}$

Area E = triangle = $\frac{1}{2}\mathrm{bh}$ $\frac{1}{2}12\times \mathrm{30}=180$

Total distance covered = Total area = 40 + 120 + 125 + 90 + 180 = 555m

(c)

$\mathrm{Average\; speed}=\frac{\mathrm{Total\; distance\; covered}}{\mathrm{Total\; time\; taken}}$

$\mathrm{Average\; speed}=\frac{\mathrm{555}}{30}$

Answer: $\mathrm{Average\; speed}=\mathrm{18.5m/s}$