Moment of a force
Moment of a force about a pivot is defined as the product of the force and the perpendicular distance of its line of action from pivot.
Moment of a force about a pivot is defined as the product of the force and the perpendicular distance of its line of action from pivot.
Formula for moment
M: Moment [Nm]
F: Force [N]
d: perpendicular distance [m]
- Perpendicular distance must be a distance from the pivot to the force.
- Perpendicular distance must be at right angle to the force.
Example
Calculate the moment of the force at the pivot.
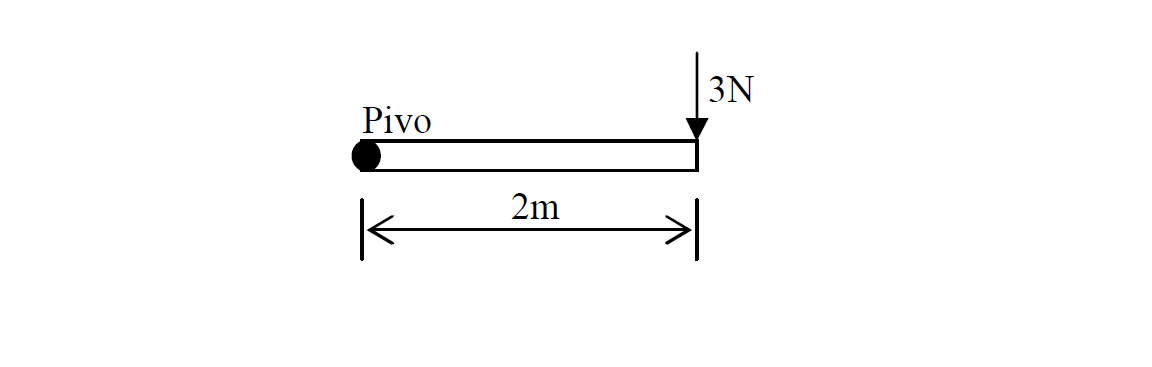
Given that
F = 3N
d = 2m
Principal of moment
Law For a body to be in equilibrium (balanced), the sum of clockwise moments about any point is equal to the sum of anticlockwise moments about the same point.
Formula
Total clockwise moment = Total anticlockwise moment
Conclusion: If a body is balanced, then the total clockwise moment is equal to the total anticlockwise moment.
Example 1
Calculate the force F if it is balance
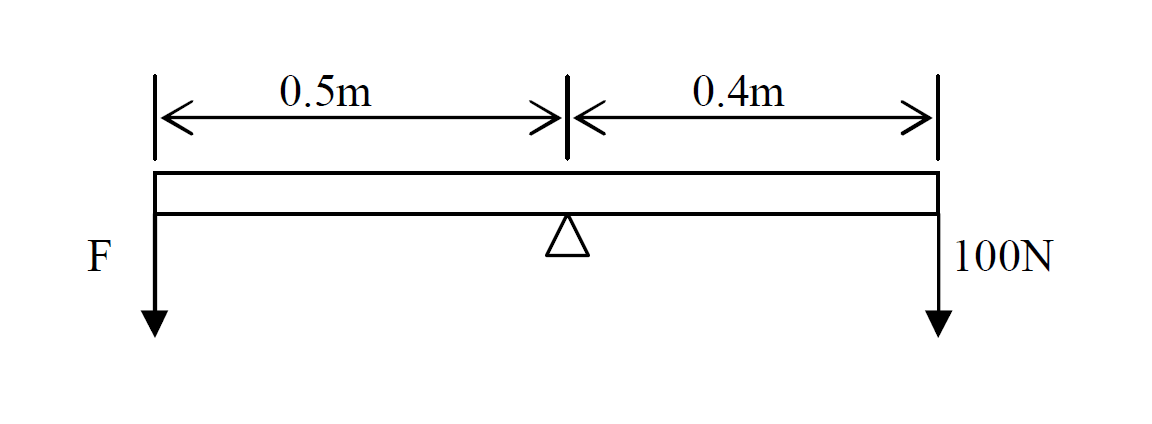
Solution
Given that
F1 = F ?
d1 = 0.5m
F2 = 100N
d2 = 0.4m
Answer:
Example 2
Calculate the distance d if it is balanced.
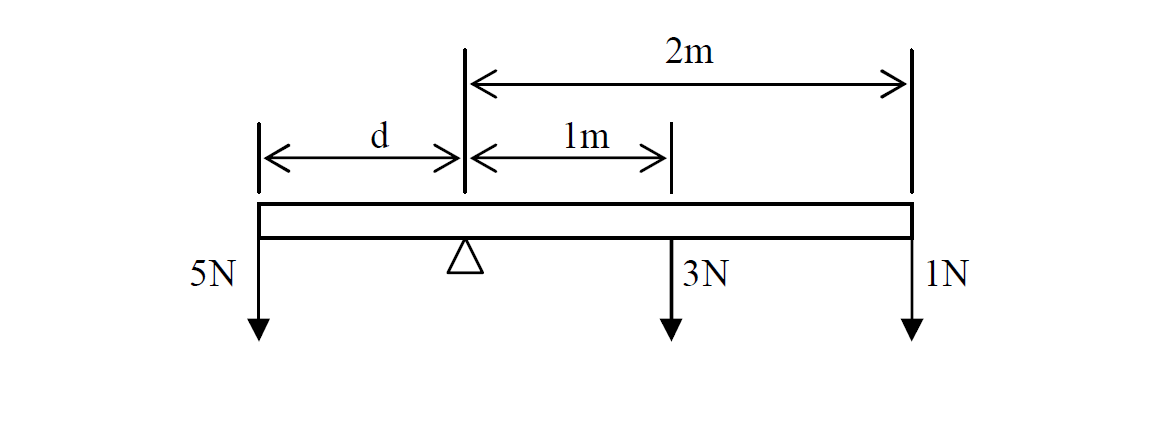
Solution
Given that
F1 = 5N
d1 = d ?
F2 = 3N, 1N
d2 = 1m , 2m
Find the two moments on the right hand side of the moment and then add those moments
= 3Nm
= 2Nm
Therefore moment on the right hand side is:
Merge the moments to find the distance d
Answer: